Mainstream labor economists as well as several public commentators have argued that trends in the economy over recent decades—including technological developments, globalization, and trade, among others—have weakened the relative earnings power of those with lower levels of skills, especially those without a college degree. In recent decades, the earnings of those with a college degree or more have risen steadily, while the wages of those with lower levels of education have stagnated or fallen. Furthermore, lifetime earnings of workers with a college degree are nearly twice as high as those without one, a point made by a number of previous Hamilton Project analyses, including one from this past year [1].
This line of reasoning leads to the view that to further the goal of widespread economic prosperity, it will be imperative to increase the skill level of many in the population, a position that a subset of us (Hershbein and Kearney) took in a recent Hamilton Project framing paper. Other commentators have objected that education is not the answer to the nation’s inequality challenge. Following up on remarks made at a recent Hamilton Project event, one of us (Summers) noted in a Washington Post interview that “to suggest that improving education is the solution to inequality is, I think, an evasion.” In this essay we clarify the different elements of the public debate and note explicitly that these positions are not necessarily at odds.
We have empirically simulated what would happen to the distribution of earnings if one out of every ten men aged 25–64 who did not have a bachelor’s degree were to instantly obtain one—a sizeable increase in college attainment. We focus on men not because women are unimportant—they clearly are important to the workforce—but because low-skilled men have seen the largest drops in employment and earnings over the past few decades, and are now considerably less likely to attend and graduate from college. We focus on college attainment because the data are readily available, but we acknowledge that it is an imperfect measure of skills, perhaps increasingly so. Despite these caveats, this empirical exercise is illuminating and sheds much needed light on an often-muddled public debate. Our analysis leads to three main takeaway points:
- Increasing the educational attainment of men without a college degree will increase their average earnings and their likelihood of being employed.
- Increasing educational attainment will not significantly change overall earnings inequality. The reason is that a large share of earnings inequality is at the top of the earnings distribution, and changing college shares will not shrink those differences.
- Increasing educational attainment will, however, reduce inequality in the bottom half of the earnings distribution, largely by pulling up the earnings of those near the 25th percentile.
These observations will not come as a surprise to most labor economists. Those of us who argue for the imperative of increasing skills are not staking out that position because we believe it will close the gap between the rich and the middle—or between the exorbitantly rich and the merely rich. Rather, we take that position because higher levels of skills will improve the economic position of those around and below the middle of the current earnings distribution. On average, more education does translate into more-valuable skills, and the results of our simulation exercise support that view. At the same time, they make it clear that increasing the share of working-age men that have college degrees will do very little to decrease the overall level of earnings inequality.
A Simulation Exercise
We conduct a simulation exercise to examine how the distribution of earned income would change if 10 percent of non-college educated men aged 25 to 64 were to immediately obtain a bachelor’s or advanced degree. To be clear, this would be a tremendous accomplishment. It is only slightly less than the observed increase in the college share over the entire 34-year period of 1979 to 2013. Furthermore, we apply this increase in educational attainment to workers regardless of age. Education policy that would tend to increase college attainment only for those newly entering the workforce would have different effects. This should be kept in mind when interpreting the simulated effects.
We carry out our analysis using the 1980 and 2014 March Current Population Survey (CPS) and we count as earned income wages and salary as well as own business income [2]. We draw from the actual distribution of annual earnings of individuals with a college or advanced degree to randomly assign these observed earnings to the new graduates. We incorporate a predicted reduction in the college wage premium in response to the increase in the relative share of the workforce with a college degree. We allow the new graduates to come from anywhere in the non-college educated distribution, meaning that we do not focus on those individuals who are closest to obtaining a college degree. This will have the effect of overstating any potential reduction in inequality.
The first two rows of Table 1 report selected percentiles of the inflation-adjusted earnings distributions for all men ages 25 to 64 in both 1979 and 2013. Notably, earnings at the 10th percentile are 0 in both years—these men did not work at all. The rise in inequality over this period is evident from the declines in earnings at the 25th and 50th percentiles, and the rise in earnings at the 75th and 90th percentiles. The changes were particularly pronounced at both ends of the distribution: earnings at the 25th percentile fell by more than half and earnings at the 90th percentile increased by one-third.
Although not shown in the table, the sharp decline in earnings at the bottom of the distribution reflects a lower likelihood of men having been employed at any point during the year; this likelihood fell from 81.6 percent in 1979 to 77.9 percent in 2013. What’s more, this decline was entirely concentrated among men without a bachelor’s degree (80.2 percent to 73.9 percent).
The third row of Table 1 shows the counterfactual case if one-tenth of the men without a college degree were to be given one, raising the share with at least a bachelor’s degree from 32 percent to 39 percent. The results indicate that earnings rise across the board, but particularly so in the bottom half of the distribution. Earnings at the 25th percentile increase from $6,100 to $8,720, and median earnings increase from $34,000 to $37,060. This is enough to nearly erase the decline in median earnings between 1979 and 2013, and cut the decline at the 25th percentile by one-third.
Although earnings also rise at the 75th and 90th percentiles, the proportional increases are smaller, and it is worth noting that the absolute gain at the 90th percentile is smaller than the absolute gain at the 25th percentile.
Table 1: Simulated effects of increasing college share on earnings distribution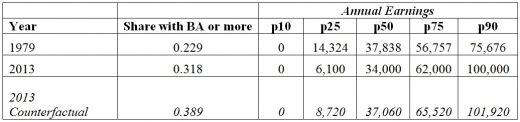
Having shown the effects of an increase in college attainment on earnings at various points in the distribution, we now turn to an examination of the impact on inequality. Increasing the share of the workforce with a college degree will have two offsetting effects on inequality. One effect will be to decrease the wage gap between those with and without a college degree, as noted above. All else equal, this will lead to a reduction in earnings inequality. However, as a group, college graduates have a wider earnings distribution than those with lower levels of education, which will lead to an offsetting increase in earnings inequality.
A summary measure of inequality that accounts for differences throughout the entire distribution is the Gini coefficient, an index that ranges from 0, if everyone has the same earnings, to 1, if a single person has all the earnings and everyone else has none. (To interpret changes in the Gini, note that under this measure of inequality, if everyone’s income increases by the same proportion, the Gini stays constant. If income increases by a larger percent at the high end, the Gini will rise.) An alternative index is the Theil index, which statistically measures the entropic “distance” of the current distribution from one in which everyone has the same income. As with the Gini, the Theil equals 0 if everyone has the same earnings; the closer the index is to 1, the more distance there is from the egalitarian position.
Table 2: Simulated results on overall earnings inequality: Gini coefficient and Theil index
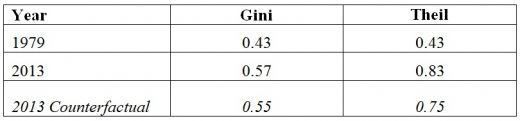
Table 2 shows the Gini coefficient and Theil index from the actual earnings distributions from 1979 and 2013, as well as from our counterfactual earnings distribution. Consistent with the pattern of changes in Table 1, these indices clearly show the increase in earnings inequality over the last three decades. However, they also make clear that overall earnings inequality would hardly change—and would not come close to 1979 levels—if the share of working-age men with a college degree were to increase by even a sizable margin.
Labor economists often examine the wage or earnings distribution by looking at ratios of different percentiles. Percentile earnings ratios have the advantages of being relatively simple to calculate and understand, and they show what is happening at different points in the earnings distribution. Several of these earnings ratios are shown in Table 3, both from the actual distributions from 1979 and 2013, and the counterfactual distribution from 2013. For example, the number in the first row and first column indicates that in 1979 someone at the 50th percentile, or median, of the earnings distribution, had earnings 2.64 times that of someone at the 25th percentile.
Table 3: Simulated effects of increasing college share on wage percentiles ratios

As we saw in Tables 1 and 2, earnings inequality increased substantially between 1979 and 2013, and this is reflected in each ratio rising considerably. However, the results of our counterfactual exercise demonstrate that increasing the share of college graduates from 32 percent to 39 percent would reduce many of these earnings ratios substantially. In particular, the three left-most ratios in Table 3, which measure inequality relative to the 25th percentile, fall by about one-third from their actual 2013 levels, and get about half-way back to their 1979 levels. These declines in part reflect the relatively large proportional increase in earnings at the 25th percentile under the counterfactual ($8,720 / $6,100 = 43 percent increase).[5]
In contrast, the p75/p50, p90/p50, and p90/p75 ratios fall only slightly, suggesting that the counterfactual does not significantly change inequality in the top half of the earnings distribution. These ratios all decline by less than 10 percent. Put differently, the increase in the share of college-educated workers benefits men with earnings at or above the median about the same in proportional terms.
Conclusion
In this analysis we have simulated the effects of increasing the college attainment of working-age men to illustrate the likely effects on earnings and earnings inequality. Our empirical simulation supports the following general observations:
- Increasing the educational attainment of men without a college degree will increase their average earnings and their likelihood of being employed.
- Increasing educational attainment will not significantly change overall earnings inequality.
- Increasing educational attainment will, however, reduce inequality in the bottom half of the earnings distribution, largely by pulling up the earnings of those near the 25th percentile.
Our nation should aim to increase the educational attainment and, more generally, the skills of less-educated and lower-income individuals because in the long-run, this is almost surely the most effective and direct way to increase their economic security, reduce poverty, and expand upward mobility. An important observation to make on this point—not captured by the empirical analysis above—is that increasing skills does not simply mean increasing the attainment of bachelor’s degrees. Increasing skills will also mean improving K-12 education and providing more training and human capital development in the specific skills demanded by the labor force.
On the other hand, additional and separate measures will be needed to address rising levels of overall inequality, which, as we have shown, is mostly driven by changes at the top of the distribution. These are distinct, albeit interrelated challenges, and the public discourse would be much improved if it stopped conflating them.
Oreopoulos and Petronijevic (2013) review the academic research on the issue and conclude that the evidence clearly suggests that higher levels of education yield substantial wage and employment benefits. Some scholars, including Beaudry, Green, and Sand (2013), have argued that the growth in the return to measured skill (education) has slowed in recent years. Nonetheless, the skill and education premium is still very large.
The March CPS asks about income from the previous calendar year, so our analysis refers to income earned in 1979 and 2013.
[3] Technical note: To incorporate this relative wage response into our simulation exercise, we have drawn on the academic literature for an estimate of such a wage elasticity: we assume that the wage premium of college-educated workers decreases by 6 percent when the relative supply of college-educated workers increases by 10 percent. This relative wage elasticity comes from the consensus estimates of Autor and Acemoglu (2010), who compare college graduates to high school graduates. (Our exercise compares men without a bachelor’s degree to those with a bachelor’s degree or more, which is somewhat broader than the educational groups used in Autor and Acemoglu.) In our exercise, we effectively change the share of men with a college degree or more from 31.8 percent to 38.9 percent (this approximately 7 percentage point difference is about one-tenth of the 68.2 percent of men who did not have at least a college degree.) Thus our exercise increases the relative supply of the college-educated from (0.318/0.682) to (0.389/0.611), or by more than 30 percent. This implies the wage premium falls by more than 18 percent (0.6 * 30). For reasonable values of the model parameters in Autor and Acemoglu (2010), the change in the wage premium is approximately evenly split between the two groups, and this is what we incorporate into our exercise, with wages of the college-educated falling by about 9 percent and wages of the less-than-college-educated rising by 9 percent. (To keep things relatively simple, we assume a constant proportional earnings change across the distribution.)
[4] Earnings have been adjusted to year 2013 dollars using the personal consumption expenditures (PCE) deflator from the Bureau of Economic Analysis (http://www.bea.gov/iTable/index_nipa.cfm, Table 1.1.4).
[5] If our simulations do not allow for the change in relative wages owing to changes in relative supply, the ratios do not decline by quite as much. Specifically, under that alternative counterfactual, the 50th/25th ratio is 4.37; the 75th/25th ratio is 8.13; and the 90th/25th ratio is 11.69.

